La réponse du Canada à la Covid-19 est guidée par les données et la modélisation mathématique. L’Agence de la santé publique du Canada (ASPC) a communiqué aux Canadiens les renseignements issus de ses travaux de modélisation de la COVID-19. Les résultats des données indiquent qu’il est indispensable et essentiel de pratiquer l’éloignement physique, de détecter et d’isoler les cas de COVID19, d’identifier et de mettre en quarantaine les contacts étroits et d’empêcher les personnes infectées à l’échelle internationale d’entrer au pays. À ce stade de l’épidémie, les efforts portent sur le contrôle de l’épidémie et l’augmentation des capacités des systèmes de soins de santé.
Résumé de la publication du Relevé des maladies transmissibles au Canada (RMTC) sur la COVID-19
Article du RMTC – Modélisation des scénarios de l’épidémie de COVID-19 au Canada
L’article décrit la modélisation prédictive de la COVID-19 en général, et les efforts déployés au sein de l’Agence de la santé publique du Canada pour modéliser les effets des interventions non pharmaceutiques (INP) sur la transmission du SARS-CoV-2 dans la population canadienne afin d’appuyer les décisions de santé publique. L’article décrit et utilise un modèle déterministe, développé dans le logiciel Analytica comme base pour fournir un synopsis des résultats liés aux différentes INP. Enfin, les taux d’hospitalisation et de mortalité sont évalués à l’aide de différents scénarios en fonction du nombre total de personnes infectées.
Téléchargez le résumé complet de l’article ici.
Glossaire des termes
Modélisation de la COVID-19 Glossaire
Utilisation et compréhension du modèle mathématique
1. Pour visualiser et exécuter ce fichier, vous aurez besoin de la version gratuite d’Analytica, disponible ici.
2. Après avoir téléchargé Analytica, téléchargez le fichier suivant :
Code de modélisation de l’ASPC pour Analytica
Le fichier devrait s’ouvrir automatiquement avec Analytica. Si des problèmes surviennent, le tutoriel suivant vous explique comment ouvrir des fichiers à l’aide du logiciel : Pour ouvrir ou quitter un modèle.
3. Téléchargez le guide d’instructions de l’ASPC : Instructions d’utilisation du modèle à compartiments COVID-19 PHAC SEIR
Description du modèle
Agence de la Santé publique du Canada COVID-19 description du modèle SEIR
La modélisation mathématique des maladies infectieuses sert principalement à étudier la propagation et la durée d’une épidémie pour comprendre l’ampleur du défi posé par la maladie et les effets potentiels des interventions. La modélisation permet aux décideurs en matière de santé publique de travailler avec des partenaires provinciaux, territoriaux et internationaux et de fonder leurs réponses aux épidémies sur les plus récentes évaluations scientifiques et situationnelles. La modélisation permet de prévoir la propagation future de la maladie au Canada et fournit une estimation du nombre possible de cas, d’hospitalisations et de décès qui pourraient survenir.
La modélisation mathématique des maladies infectieuses sert principalement à étudier la propagation et la durée d’une épidémie pour comprendre l’ampleur du défi posé par la maladie et les effets potentiels des interventions. La modélisation permet aux décideurs en matière de santé publique de travailler avec des partenaires provinciaux, territoriaux et internationaux et de fonder leurs réponses aux épidémies sur les plus récentes évaluations scientifiques et situationnelles. La modélisation permet de prévoir la propagation future de la maladie au Canada et fournit une estimation du nombre possible de cas, d’hospitalisations et de décès qui pourraient survenir.
Dans un modèle susceptible-exposé-infectieux–retiré (modèle SEIR) :
Les personnes susceptibles (S) n’ont jamais été infectées par l’agent pathogène et peuvent donc être infectées.
Les personnes exposées (E) ont été infectées par un agent pathogène, mais elles ne sont pas encore infectieuses, en raison de la période de latence de la maladie.
Les personnes infectieuses (I) sont infectées et sont capables de transmettre l’agent pathogène à d’autres.
Les personnes retirées (R) ne sont plus capables de transmettre la maladie. Ce groupe comprend les personnes rétablies et les décès.
La logique, les hypothèses et la structure du modèle sont résumées et illustrées dans la figure 1. Comme ce virus est un virus auquel l’homme n’a jamais été exposé auparavant, l’hypothèse de base est que toute la population se trouve au départ dans le compartiment susecptible. Dans les conditions initiales, des personnes infectieuses sont introduites dans la population, ce qui « amorce » l’épidémie. Les taux de contact entre les personnes, combinés au nombre d’individus infectieux et susceptibles dans la population, sont utilisés pour calculer la probabilité qu’une personne susceptible et une personne infectieuse entrent en contact dans un laps de temps limité. Cette probabilité est ensuite combinée à la probabilité que le contact ait été infecté, pour estimer la vitesse à laquelle les personnes susceptibles se déplacent dans le compartiment exposé.
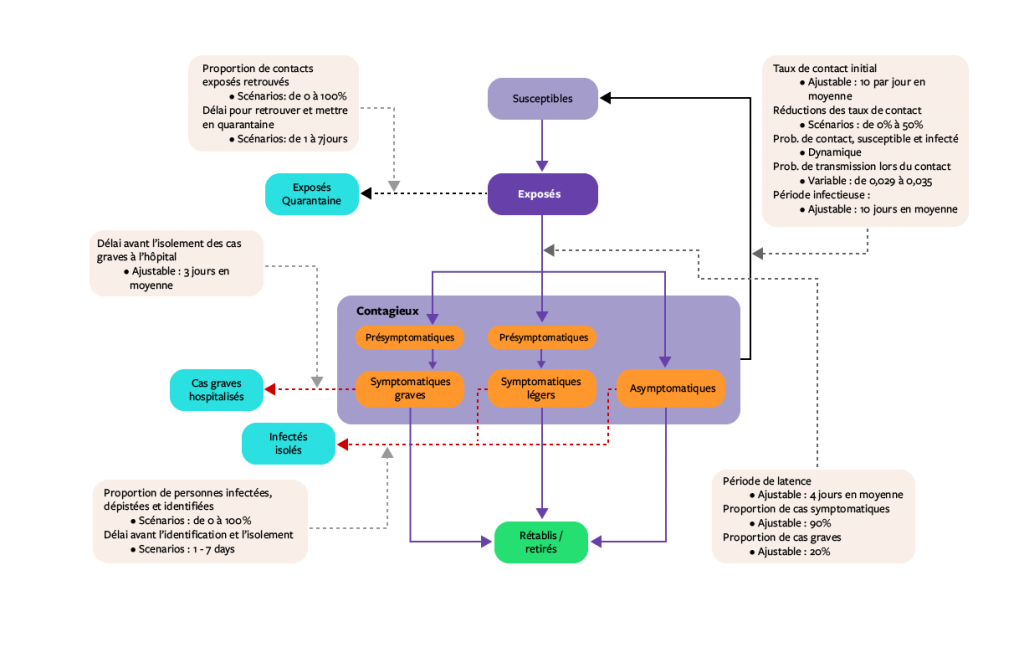
Par la suite, la progression des personnes dans le modèle, du compartiment exposé aux stades infectieux grave, infectieux léger ou infectieux asymptomatique, est dictée à la fois par la période de latence et par la proportion de cas estimés asymptomatiques, graves ou légers. Les estimations sont tirées d’études menées dans différents pays déjà touchés par l’épidémie. La période infectieuse dicte alors la vitesse à laquelle la population infectieuse progresse vers le compartiment rétabli/retiré. À ce stade, une des hypothèses clés est que la population reste immunisée contre toute nouvelle infection pendant la durée de la période modélisée.
Parmi les facteurs clés qui modifient le taux de transmission et les résultats finaux prévus par le modèle, mentionnons les suivants :
- Les effets des mesures de distanciation physique ont un impact sur les taux de contact.
- Les personnes exposées sont mises en quarantaine grâce à la recherche des contacts.
- Les personnes présentant des symptômes infectieux graves sont hospitalisées et, de ce fait, sont isolées et ne propagent plus l’infection dans la communauté.
- Les personnes légèrement symptomatiques et asymptomatiques sont isolées à la suite de l’augmentation des tests dans la communauté.
Le modèle utilise les meilleures estimations pour certains paramètres, qui peuvent être remplacées par des distributions théoriques (plage) afin de refléter l’incertitude. En outre, le modèle permet naturellement de faire une analyse paramétrique lorsqu’une gamme de valeurs de paramètres est utilisée avant de visualiser les résultats.